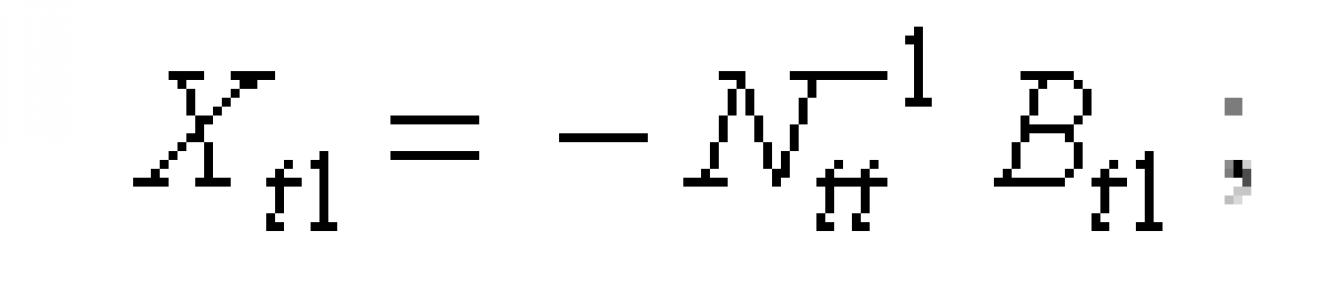Násobení soustavy normálních rovnic NttXt1 + Bt1 = 0 inverzní maticí N-1

dostávat:

(34)

(35)

Řešení normálních rovnic inverzní metodou.

Podle definice inverzní matice je N-1N = E. Tato rovnost se používá k odůvodnění metody určování prvků inverzní matice. Nechť t = 2.

Z toho vyplývá:

- 1. soustava vážených normálních rovnic.

- 2. soustava vážených normálních rovnic.

V obecném případě, jako výsledek takových akcí, bude získáno t systémů vážených normálních rovnic, s t rovnic v každém systému. Tyto systémy mají stejnou matici koeficientů jako hlavní, s neznámými δхj a liší se od ní pouze ve sloupcích volných členů. V j-té rovnici j-té soustavy je volný člen -1, zbytek je roven nule. Soustavy vážených normálních rovnic jsou řešeny paralelně s hlavním systémem, v obecném schématu s použitím dalších sloupců pro volné členy těchto systémů (tab. 9). Pro kontrolu jsou vypočtené hodnoty prvků inverzní matice Qij dosazeny do souhrnných rovnic sestavených pro váhové systémy. Například pro t = 2 budou tyto rovnice vypadat takto:

( + [rab]) Q11 + ( + ) Q12-1 = 0;

( + ) Q21 + ( + ) Q22 - 1 = 0.

Pro předběžnou kontrolu se použijí rovnosti Qij = Qji (i ≠ j).

Prvky inverzní matice Qij se nazývají váhové koeficienty.

Tabulka 9

Určení prvků inverzní matice v Gaussově schématu

3.6. Posouzení přesnosti na základě vyrovnávacích materiálů

Střední kvadratická chyba funkce parametru je určena vzorcem:

Kde

(36)

střední kvadratická chyba jednotkové hmotnosti;

(37)

Inverzní váha funkce parametrů nebo ve formě matice:

(38)

Inverzní váha parametru rovna diagonálnímu prvku inverzní matice.

3.7. Blokové schéma metody parametrického vyrovnání

1. Analyzujte soubor měření yi, určete t - počet požadovaných měření. Sestavte systém měřících stupnic pi (i = 1, 2, ..., n).

2. Vyberte nezávislé parametry x1, x2, ..., xt, jejichž počet je roven t.

3. Sestavte parametrické komunikační rovnice. Vyrovnané hodnoty všech měřených veličin jsou vyjádřeny jako funkce vybraných parametrů.

4. Najděte přibližné hodnoty parametrů x0j.

5. Parametrické vazebné rovnice jsou redukovány na lineární formu, jsou vypočteny koeficienty a volné členy parametrických korekčních rovnic.

6. Sestrojte funkci parametrů pro vyhodnocení její přesnosti. Váhová funkce je linearizována.

7. Sestavte normální rovnice, vypočítejte koeficienty a volné členy normálních rovnic.

8. Řešte normální rovnice, počítejte korekce na přibližné hodnoty parametrů a kontrolujte je.

9. Jsou vypočteny korekce vi výsledků měření a νi a jsou monitorovány.

10. Vypočítejte parametry, upravené výsledky měření a proveďte kontrolu nastavení.

11. Vypočítejte inverzní váhy parametrů a funkcí parametrů.

12. Vyhodnoťte přesnost výsledků měření a vypočítejte střední kvadratickou chybu jednotky hmotnosti.

13. Vypočítejte střední kvadratické chyby ekvalizovaných veličin.

řešit matematiku. Najděte rychle řešení matematické rovnice v režimu online. Web www.site to umožňuje řešit rovnici téměř jakýkoli daný algebraický, trigonometrický nebo transcendentální rovnice online. Při studiu téměř jakéhokoli oboru matematiky v různých fázích se musíte rozhodnout rovnice online. Abyste dostali odpověď okamžitě, a hlavně přesnou odpověď, potřebujete zdroj, který vám to umožní. Díky webu www.site řešit rovnice online bude trvat několik minut. Hlavní výhoda www.site při řešení matematických rovnice online- jedná se o rychlost a přesnost poskytnuté odpovědi. Stránka je schopna vyřešit jakékoli algebraické rovnice online, goniometrické rovnice online, transcendentální rovnice online, a rovnic s neznámými parametry v režimu online. Rovnice slouží jako výkonný matematický aparát řešení praktické problémy. S pomocí matematické rovnice je možné vyjádřit fakta a vztahy, které se na první pohled mohou zdát matoucí a složité. Neznámé množství rovnic lze nalézt formulací problému v matematický jazyk ve formuláři rovnic A rozhodni se přijatý úkol v režimu online na webu www.site. Žádný algebraická rovnice, goniometrická rovnice nebo rovnic obsahující transcendentální funkce, které můžete snadno rozhodni se online a získejte přesnou odpověď. Při studiu přírodních věd se nevyhnutelně setkáváte s potřebou řešení rovnic. V tomto případě musí být odpověď přesná a musí být získána okamžitě v režimu online. Proto pro řešení matematických rovnic online doporučujeme stránku www.site, která se stane vaší nepostradatelnou kalkulačkou řešit algebraické rovnice online, goniometrické rovnice online, a transcendentální rovnice online nebo rovnic s neznámými parametry. Pro praktické problémy hledání kořenů různých matematické rovnice zdroj www.. Řešení rovnice online sami, je užitečné zkontrolovat přijatou odpověď pomocí online řešení rovnic na webu www.site. Musíte napsat rovnici správně a okamžitě ji získat online řešení, po kterém už zbývá jen porovnat odpověď s vaším řešením rovnice. Kontrola odpovědi nezabere déle než minutu, to stačí řešit rovnice online a porovnejte odpovědi. To vám pomůže vyhnout se chybám rozhodnutí a včas opravit odpověď řešení rovnic online buď algebraický, trigonometrický, transcendentální nebo rovnice s neznámými parametry.

Jedna z nejdůležitějších dovedností, kdy přijetí do 5. třídy je schopnost řešit jednoduché rovnice. Od 5. třídy ještě není tak daleko základní škola, pak není tolik typů rovnic, které student dokáže vyřešit. Seznámíme vás se všemi základními typy rovnic, které pokud chcete, musíte umět řešit nastoupit na fyzikální a matematickou školu.

Typ 1: "cibulovitý"
To jsou rovnice, se kterými se téměř pravděpodobně setkáte přijetí na jakoukoli školu nebo kroužek 5. třídy jako samostatný úkol. Jsou snadno odlišitelné od ostatních: v nich je proměnná přítomna pouze jednou. Například, nebo.
Jsou řešeny velmi jednoduše: stačí se „dostat“ do neznáma, postupně „odstraňovat“ vše nepotřebné, co ho obklopuje – jako byste loupali cibuli – odtud název. Chcete-li to vyřešit, stačí si zapamatovat pár pravidel z druhé třídy. Pojďme si je všechny vyjmenovat:

Přidání

člen1 + člen2 = součet
člen1 = součet - člen2
člen2 = součet - člen1

Odčítání

minuend - subtrahend = rozdíl
minuend = subtrahend + rozdíl
subtrahend = minuend - rozdíl

Násobení

faktor1 * faktor2 = produkt
faktor1 = produkt: faktor2
faktor2 = produkt: faktor1

Divize

dividenda: dělitel = podíl
dividenda = dělitel * kvocient
dělitel = dělenec: podíl

Podívejme se na příklad, jak tato pravidla aplikovat.

Všimněte si, že se rozdělujeme na a přijímáme . V této situaci známe dělitele a podíl. Chcete-li najít dividendu, musíte vynásobit dělitele kvocientem:

Trochu jsme se přiblížili sami sobě. Teď to vidíme je přidáno a ukazuje se . To znamená, že abyste našli jeden z výrazů, musíte od součtu odečíst známý výraz:

A další „vrstva“ byla odstraněna z neznáma! Nyní vidíme situaci se známou hodnotou součinu () a jedním známým multiplikátorem ().

Nyní je situace „minuend - subtrahend = rozdíl“

A posledním krokem je známý produkt () a jeden z faktorů ()

Typ 2: rovnice se závorkami
Rovnice tohoto typu se nejčastěji vyskytují v úlohách – 90 % všech úloh pro přijetí do 5. třídy. Na rozdíl od "cibulové rovnice" proměnná se zde může objevit vícekrát, takže není možné ji řešit metodami z předchozího odstavce. Typické rovnice: nebo
Hlavním problémem je správné otevření držáků. Poté, co jste to zvládli správně, měli byste redukovat podobné pojmy (čísla na čísla, proměnné na proměnné) a poté dostaneme nejjednodušší "cibulová rovnice" které můžeme vyřešit. Ale nejdřív.

Rozšíření závorek. Dáme pár pravidel, která by se měla používat v tomto případě. Ale jak ukazuje praxe, student začne správně otevírat závorky až po 70-80 dokončených problémech. Základní pravidlo je toto: jakýkoli faktor mimo závorku musí být vynásoben každým členem uvnitř závorky. A znaménko mínus před závorkou změní znaménko všech výrazů uvnitř. Takže základní pravidla zveřejňování:

Přinášet podobné. Zde je vše mnohem snazší: musíte převodem podmínek přes rovnítko zajistit, aby na jedné straně byly pouze termíny s neznámým a na druhé straně pouze čísla. Základní pravidlo je toto: každý termín přenesený prostřednictvím změní své znaménko - pokud byl s, stane se s a naopak. Po úspěšném převodu je nutné spočítat celkový počet neznámých, celkový počet na druhé straně rovnosti než proměnné a vyřešit jednoduchý "cibulová rovnice".

Rovnice je rovnost, ve které je neznámý člen - x. Jeho smysl je třeba najít.

Neznámá veličina se nazývá kořen rovnice. Řešení rovnice znamená najít její kořen a k tomu potřebujete znát vlastnosti rovnic. Rovnice pro ročník 5 nejsou těžké, ale pokud se je naučíte správně řešit, nebudete s nimi mít v budoucnu problémy.

Hlavní vlastnost rovnic

Když se obě strany rovnice změní o stejnou hodnotu, zůstává to stále stejná rovnice se stejným kořenem. Pojďme vyřešit několik příkladů, abychom toto pravidlo lépe pochopili.

Jak řešit rovnice: Sčítání nebo odčítání

Předpokládejme, že máme rovnici ve tvaru:

a + x = b - zde a a b jsou čísla a x je neznámý člen rovnice.

Pokud přičteme (nebo od nich odečteme) hodnotu c na obě strany rovnice, nezmění se:

a + x + c = b + c
a + x - c = b - c.

Příklad 1

Použijme tuto vlastnost k vyřešení rovnice:

37+x=51

Odečtěte číslo 37 z obou stran:

37+x-37=51-37

dostaneme:

x = 51-37.

Kořen rovnice je x=14.

Když se pozorně podíváme na poslední rovnici, vidíme, že je stejná jako ta první. Jednoduše jsme přesunuli člen 37 z jedné strany rovnice na druhou a nahradili jsme plus mínusem.

Ukazuje se, že libovolné číslo lze přenést z jedné části rovnice do druhé s opačným znaménkem.

Příklad 2

37+x=37+22

Proveďme stejnou akci, přesuňte číslo 37 z levé strany rovnice doprava:

x=37-37+22

Protože 37-37=0, jednoduše to snížíme a dostaneme:

x = 22.

Identické členy rovnice se stejným znaménkem, umístěné v různých částech rovnice, lze redukovat (přeškrtnout).

Násobící a rozdělovací rovnice

Obě strany rovnosti lze také vynásobit nebo vydělit stejným číslem:

Pokud se rovnost a = b vydělí nebo vynásobí c, nezmění se:

a/c = b/c,
ac = bс.

Příklad 3

5x = 20

Vydělme obě strany rovnice 5:

5x/5 = 20/5.

Protože 5/5 = 1, snížíme tyto násobitele a dělitele na levé straně rovnice a dostaneme:

x = 20/5, x = 4

Příklad 4

5x = 5a

Pokud jsou obě strany rovnice dělené 5, dostaneme:

5x/5 = 5a/5.

Číslo 5 v čitateli a jmenovateli levé a pravé strany je zrušeno, takže x = a. To znamená, že identické faktory na levé a pravé straně rovnic se ruší.

Řešíme další příklad:

13 + 2x = 21

Posouváme člen 13 z levé strany rovnice doprava s opačným znaménkem:

2x = 21-13
2x = 8.

Vydělením obou stran rovnice 2 dostaneme:

x = 4.

Rovnice s jednou neznámou, která po otevření závorek a uvedení podobných pojmů nabývá tvaru

ax + b = 0, kde a a b jsou libovolná čísla, se nazývá lineární rovnice s jednou neznámou. Dnes zjistíme, jak tyto lineární rovnice vyřešit.

Například všechny rovnice:

2x + 3= 7 – 0,5x; 0,3x = 0; x/2 + 3 = 1/2 (x – 2) - lineární.

Hodnota neznámé, která změní rovnici na skutečnou rovnost, se nazývá rozhodnutí nebo kořen rovnice .

Pokud například v rovnici 3x + 7 = 13 místo neznámého x dosadíme číslo 2, dostaneme správnou rovnost 3 2 +7 = 13. To znamená, že hodnota x = 2 je řešením nebo kořenem rovnice.

A hodnota x = 3 nemění rovnici 3x + 7 = 13 ve skutečnou rovnost, protože 3 2 +7 ≠ 13. To znamená, že hodnota x = 3 není řešením ani kořenem rovnice.

Řešení jakéhokoliv lineární rovnice redukuje na řešení rovnic tvaru

ax + b = 0.

Přesuneme volný člen z levé strany rovnice doprava a změníme znaménko před b na opačné, dostaneme

Pokud a ≠ 0, pak x = ‒ b/a .

Příklad 1 Řešte rovnici 3x + 2 =11.

Přesuneme 2 z levé strany rovnice doprava a změníme znaménko před 2 na opačné, dostaneme
3x = 11 – 2.

Tak pojďme na odčítání
3x = 9.

Chcete-li najít x, musíte vydělit součin známým faktorem, tzn
x = 9:3.

To znamená, že hodnota x = 3 je řešením nebo kořenem rovnice.

Odpověď: x = 3.

Pokud a = 0 a b = 0, pak dostaneme rovnici 0x = 0. Tato rovnice má nekonečně mnoho řešení, protože když vynásobíme libovolné číslo 0, dostaneme 0, ale b se také rovná 0. Řešením této rovnice je libovolné číslo.

Příklad 2 Vyřešte rovnici 5(x – 3) + 2 = 3 (x – 4) + 2x ‒ 1.

Rozbalíme závorky:
5x – 15 + 2 = 3x – 12 + 2x ‒ 1.

5x – 3x ‒ 2x = – 12 ‒ 1 + 15 ‒ 2.

Zde jsou některé podobné výrazy:
0x = 0.

Odpověď: x - libovolné číslo.

Pokud a = 0 a b ≠ 0, pak dostaneme rovnici 0x = - b. Tato rovnice nemá řešení, protože když vynásobíme libovolné číslo 0, dostaneme 0, ale b ≠ 0.

Příklad 3 Vyřešte rovnici x + 8 = x + 5.

Seskupme termíny obsahující neznámé na levé straně a volné termíny na pravé straně:
x – x = 5 – 8.

Zde jsou některé podobné výrazy:
0х = ‒ 3.

Odpověď: žádná řešení.

Na Obrázek 1 ukazuje schéma řešení lineární rovnice

Sestavme si obecné schéma řešení rovnic s jednou proměnnou. Podívejme se na řešení příkladu 4.

Příklad 4. Předpokládejme, že potřebujeme vyřešit rovnici

1) Vynásobte všechny členy rovnice nejmenším společným násobkem jmenovatelů rovným 12.

2) Po zmenšení dostaneme
4 (x – 4) + 3 2 (x + 1) ‒ 12 = 6 5 (x – 3) + 24x – 2 (11x + 43)

3) Chcete-li oddělit výrazy obsahující neznámé a volné výrazy, otevřete hranaté závorky:
4x – 16 + 6x + 6 – 12 = 30x – 90 + 24x – 22x – 86.

4) Seskupme do jedné části termíny obsahující neznámé a do druhé volné termíny:
4x + 6x – 30x – 24x + 22x = ‒ 90 – 86 + 16 – 6 + 12.

5) Uveďme podobné pojmy:
-22x = -154.

6) Vydělte – 22, dostaneme
x = 7.

Jak vidíte, kořen rovnice je sedm.

Obecně takové rovnice lze řešit pomocí následujícího schématu:

a) převést rovnici do jejího celočíselného tvaru;

b) otevřete závorky;

c) seskupit členy obsahující neznámou v jedné části rovnice a volné členy ve druhé;

d) přivést podobné členy;

e) řešit rovnici tvaru aх = b, která byla získána po přivedení podobných členů.

Toto schéma však není nutné pro každou rovnici. Při řešení mnoha jednodušších rovnic musíte začít ne od první, ale od druhé ( Příklad. 2), Třetí ( Příklad. 13) a dokonce od páté fáze, jako v příkladu 5.

Příklad 5.Řešte rovnici 2x = 1/4.

Najděte neznámou x = 1/4: 2,
x = 1/8 .

Podívejme se na řešení některých lineárních rovnic nalezených v hlavní státní zkoušce.

Příklad 6.Řešte rovnici 2 (x + 3) = 5 – 6x.

2x + 6 = 5 – 6x

2x + 6x = 5 – 6

Odpověď: - 0,125

Příklad 7. Vyřešte rovnici – 6 (5 – 3x) = 8x – 7.

– 30 + 18x = 8x – 7

18x – 8x = – 7 +30

Odpověď: 2.3

Příklad 8. Vyřešte rovnici